酵素反応と速度論

1.はじめに

　生体は有機物であり，生命の活動の根底にあるものは化学反応です．生物を構成する物質は例えばDNA（デオキシリボ核酸），タンパク質，糖類そして脂質などです．タンパク質には化学反応を触媒する酵素が含まれており，生体内の様々な代謝活動に関与します．この酵素の働きは発酵というかたちで利用されてきました．身近では，微生物による乳製品の製造や醸造などがあります．それにとどまらず，食品や医薬品の製造そしてバイオマスへの利用など，幅広く工業に応用されています．また洗剤には“酵素パワー”と謳っているように，タンパク質や油そしてデンプンを分解する酵素が含まれているものもあります．

　生体の運動も酵素活性に由来していますので，医学や生理学分野においてもこれらの働きを知ることは重要です．最近では遺伝工学の発展により，組み換え型の酵素も生産可能になっています．そこで，自動車の設計にはエンジンの性能テストが必要なように，酵素の性能テストが行われます．エンジンの場合には回転数，トルク，パワーのような特性を，酵素の場合には活性（１分子単位時間あたりの回転数）や親和性（反応物質と酵素の結合のしやすさ）などが測定されます．このような解析において，数学の知識は必要になってきます．まずは，もっとも単純な化学反応の例から始めましょう．

図1 アデノシン三リン酸分解酵素−ミオシンの原子モデル．およそ900個のアミノ酸が直鎖状につながったものが，その配列に従って立体構造をつくります．この場合，約20ナノメートルの長さです．

２．反応速度

(1) Aという物質がBという物質に変化する反応を考えてます（BからAには戻らないとします）．

　　　　　　　　　　　　　　　　　　　　　　　　　　 ---- (1)　　　　

[　] は物質の濃度を表します．

このとき，[A]が減少する速度が[A]に比例することが知られています．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ---- (2)

ここで，Vは[A]の減少速度であり，は速度定数と呼ばれる反応に固有な値です．

(2) 次に，AとBが反応してCという物質に変化し，その逆の変化もある場合を考えます（正反応の速度定数をとし，逆反応の速度定数をとします）．

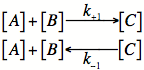　　　　　　　　　　　　　　　　　　　　　 ---- (3)

このとき，Cの生成速度は次のようになります．

　　　　　　　　　　　　　　　　　　 ---- (4)

そして反応が十分にすすんで，反応速度が零になったときを平衡状態と呼びます．

　　　　 ---- (5)

速度定数の比は平衡定数（）と呼ばれ一定の値です．[A], [B], [C] は平衡に達するように自発的に変化します．平衡定数が大きいほど反応は進みやすいといえます．

【問１】　酸性条件下でショ糖はブドウ糖と果糖に加水分解します．この反応が不可逆であるとしたとき，反応開始からの時間tとショ糖濃度[S]の関係を式にしなさい．但し，速度定数を，反応開始時間（t = 0）でのショ糖濃度を[]とします．

3.酵素反応

　酵素は，一見すると物質の合成や分解をするように思えますが，物質がもつ平衡状態に速く近づけるものです．これを触媒と呼びます．酵素と結合して触媒される物質を基質と呼びます．もっとも単純な酵素反応は次のようになります（生成物からの逆反応は通常小さいので，ここでは省略します）．

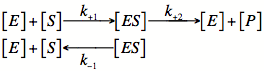　　　　　　 ---- (6)

それぞれ， [E]は酵素，[S]は基質，[ES]は酵素基質の複合体，[P]は生成物の濃度を示します．, , は反応過程での速度定数です．は律速過程であり，多くの場合となります．この反応における[ES]の生成速度と[P]の生成速度について式をたてます．

　　　　　　　　　　　　　 ---- (7)

　　　　　　　　　　　　　　　　　　　　　　　　 ---- (8)

酵素の初期濃度を[E₀]とし（[E₀]=[ES]+[E]），[ES]は反応後に定常状態になると考えると，

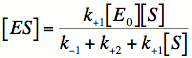　　　　　　　　　　　　　　　　　　　　　　　 ---- (9)

となります．式(9)を式(8)に代入すると，

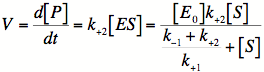　　　　　　 　　　　　　　 ---- (10)

の関係式を導けます．Vは[P]の生成速度で，[S]の関数になります（図2-1）．これは1913年にミカエリスとメンテンが導入した式（Michaelis-Mentenの式）です．

さらに式(10)の右辺について， [S]を無限大にすると，

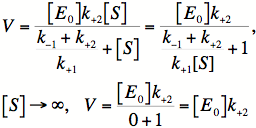　　　　　　　　　　　　　　　 --- (11)

となります．は定数であり， [S]が無限大のときの速度（最大速度）に相当します．

はミカエリス定数と呼ばれ，酵素基質の見かけの親和性を意味します．

　さて，実験的にとを求めるために，様々な[S]で速度を測定します．そして結果の見通しをよくするために式を変形してグラフにプロットすることがあります．この場合には両辺の逆数をとりプロットします（図2-2）．これは1934年にラインウィバーとバーグが開発した方法です（Lineweaver-Burkの二重逆数プロット）．

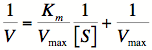　　　　　　　　　　　　　　　　　　　　 --- (12)

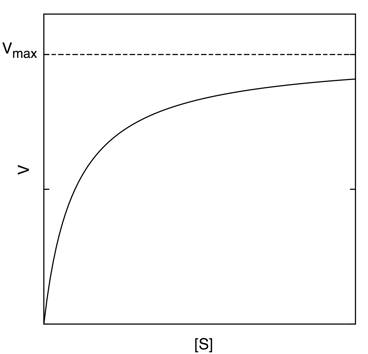
図2-1 基質濃度と反応速度

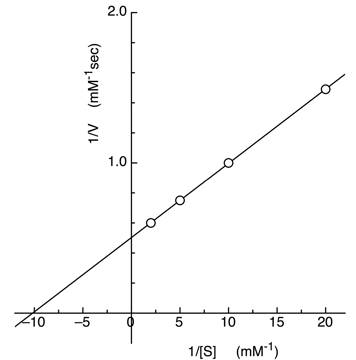
図2-2 二重逆数プロット

【問２】　図2-2においてとを読み取りなさい．また基質の濃度がのときの速度はの何倍になるか．

3. 反応速度と温度

　化学反応は温度が高いほど，促進されることは日常的にわかります．例えば私たちは食品をなるべく腐敗や分解（化学反応）させないように冷蔵庫に保管します．温度と反応速度定数の間に次の関係があることがわかっています．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ---- (13)

kは速度定数（sec^—１），Tは温度(K)，Eaは活性化エネルギー（J mol^—１），Rは気体定数（8.314 JK^—１mol^—１）です．これは1889年にアレニウスが導入した式（Arrheniusの式）です．

この式を積分すると，

　　　　　　　　　　　　　　　　　　　　　　　　　　 ---- (14)

となり，速度定数は温度の逆数の指数関数になります（図3-1）．Aは頻度因子と呼びます．頻度因子は運動する分子の衝突数であり，その中で活性化エネルギーを超えた運動エネルギーをもつ分子が反応しうると解釈できます．実際には，もっと複雑な要因がありますが，比較的低温では実験結果と合うことが知られています．さらにこの式の両辺を対数にとり，対数-逆数プロットすると関係がわかりやすくなります（式(15)，図3-2）．

　　　　　　　　　　　　　　　　　　　　　 ---- (15)

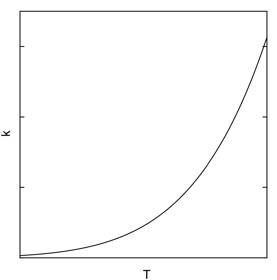
図3-1 温度と反応速度

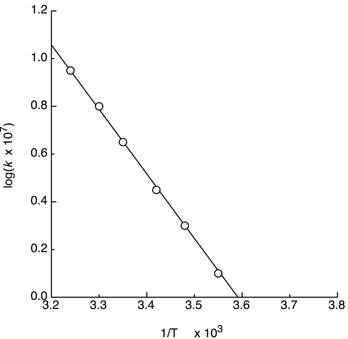
図3-2対数−逆数によるArrheniusの式のプロット（ミオシンATPaseの場合）

【問３】式(15)を導きなさい．図3-2におけるプロットから活性化エネルギーを求めなさい．

4. おわり

　酵素反応のもっとも単純なかたちをみてきました．実際には高次反応や多数の経路を取り扱うことが多くなります．また平衡過程だけではなく，反応の過渡状態も議論することもあります．生物の代謝は化学反応が複雑に絡まり合ったものです．その解析のためにはさらに微分方程式の知識が必要になることでしょう．

参考文献

中村隆雄 著，酵素 反応速度論と機構，学会出版センター